Sessellift
About points...
We associate a certain number of points with each exercise.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
When you click an exercise into a collection, this number will be taken as points for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit the number of points for the exercise in the collection independently, without any effect on "points by default" as represented by the number here.
That being said... How many "default points" should you associate with an exercise upon creation?
As with difficulty, there is no straight forward and generally accepted way.
But as a guideline, we tend to give as many points by default as there are mathematical steps to do in the exercise.
Again, very vague... But the number should kind of represent the "work" required.
About difficulty...
We associate a certain difficulty with each exercise.
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
When you click an exercise into a collection, this number will be taken as difficulty for the exercise, kind of "by default".
But once the exercise is on the collection, you can edit its difficulty in the collection independently, without any effect on the "difficulty by default" here.
Why we use chess pieces? Well... we like chess, we like playing around with \(\LaTeX\)-fonts, we wanted symbols that need less space than six stars in a table-column... But in your layouts, you are of course free to indicate the difficulty of the exercise the way you want.
That being said... How "difficult" is an exercise? It depends on many factors, like what was being taught etc.
In physics exercises, we try to follow this pattern:
Level 1 - One formula (one you would find in a reference book) is enough to solve the exercise. Example exercise
Level 2 - Two formulas are needed, it's possible to compute an "in-between" solution, i.e. no algebraic equation needed. Example exercise
Level 3 - "Chain-computations" like on level 2, but 3+ calculations. Still, no equations, i.e. you are not forced to solve it in an algebraic manner. Example exercise
Level 4 - Exercise needs to be solved by algebraic equations, not possible to calculate numerical "in-between" results. Example exercise
Level 5 -
Level 6 -
Question
Solution
Short
Video
\(\LaTeX\)
Need help? Yes, please!
The following quantities appear in the problem:
The following formulas must be used to solve the exercise:

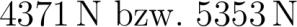
No explanation / solution video to this exercise has yet been created.
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Visit our YouTube-Channel to see solutions to other exercises.
Don't forget to subscribe to our channel, like the videos and leave comments!
Exercise:
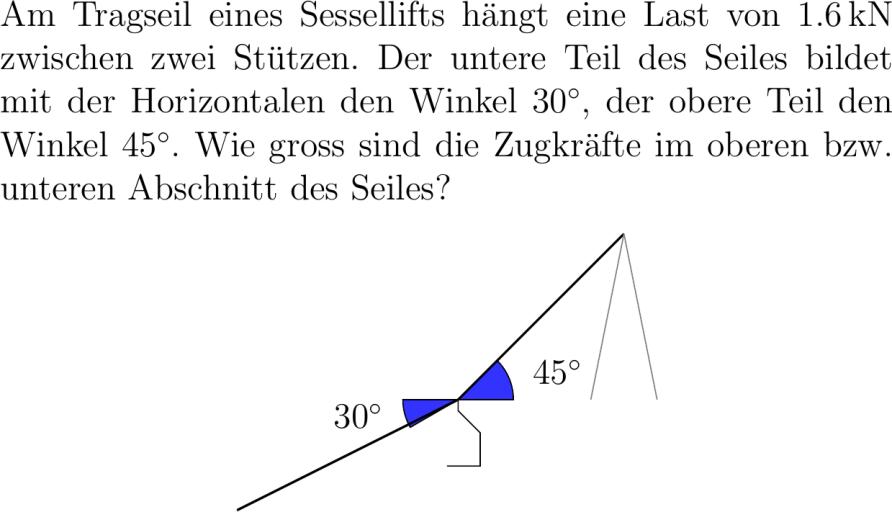
Am Tragseil eines Sessellifts hängt eine Last von .kN zwischen zwei Stützen. Der untere Teil des Seiles bildet mit der Horizontalen den Winkel ang der obere Teil den Winkel ang. Wie gross sind die Zugkräfte im oberen bzw. unteren Abschnitt des Seiles? center tikzpicturescale. filldrawfillblue!!white --. arc::.--cycle; filldrawfillblue!!white ---. arc::.--cycle; node at .. ang; node at -.-. ang; drawthick --..; drawthick ----; draw ---.--.-.--.-.---.-.; drawcolorblack!!white ..--.; drawcolorblack!!white ..--.; tikzpicture center
Solution:
newcommandFreF_rightarrow newcommandFliF_leftarrow newcommandFobF_uparrow newcommandFunF_downarrow newcommandFZliF_swarrow newcommandFZreF_nearrow newcommandFZliliF_swarrowleftarrow newcommandFZliunF_swarrowdownarrow newcommandFZrereF_nearrowrightarrow newcommandFZreobF_nearrowuparrow Es muss sowohl in horizontale als in vertikale Richtung Kräftegleichgewicht herrschen: center multicols edt Fli &mustbe Fre FZlili FZrere FZlicosalpha FZrecosbeta ed edt Fob &mustbe Fun FZreob FG + FZliun FZre sinbeta FG + FZlisinalpha ed multicols center Die untersten beiden Gleichungen bilden ein Gleichungssystem mit den Unbekannten FZli und FZre: al FZlicosalpha FZrecosbeta FZre sinbeta FG + FZlisinalpha. Wir lösen die eine Gleichung egal welche -- wir wählen die erste weil sie einfacher aussieht nach der einen Unbekannten egal welche -- wir wählen FZli auf: al FZlicosalpha FZrecosbeta uf:cosalpha FZli fracFZrecosbetacosalpha. Diesen Ausdruck setzen wir in die andere Gleichung ein und lösen nach der anderen Unbekannten FZre auf: al FZre sinbeta FG + FZlisinalpha es FZre sinbeta FG + fracFZrecosbetacosalpha sinalpha tu FZre sinbeta FG + FZrecosbeta tanalpha uf-FZrecosbetatanalpha FZresinbeta - cosbetatanalpha FG uf:sinbeta - cosbetatanalpha FZre fracFGsinbeta - cosbetatanalpha frac.eNsindegree - cosdegree tandegree .kN Wir setzen das Ergebnis in die nach der anderen Unbekannten FZli aufgelösten Gleichung ein: al FZli fracFZrecosbetacosalpha frac.eN cosdegreecosdegree .kN.
Am Tragseil eines Sessellifts hängt eine Last von .kN zwischen zwei Stützen. Der untere Teil des Seiles bildet mit der Horizontalen den Winkel ang der obere Teil den Winkel ang. Wie gross sind die Zugkräfte im oberen bzw. unteren Abschnitt des Seiles? center tikzpicturescale. filldrawfillblue!!white --. arc::.--cycle; filldrawfillblue!!white ---. arc::.--cycle; node at .. ang; node at -.-. ang; drawthick --..; drawthick ----; draw ---.--.-.--.-.---.-.; drawcolorblack!!white ..--.; drawcolorblack!!white ..--.; tikzpicture center
Solution:
newcommandFreF_rightarrow newcommandFliF_leftarrow newcommandFobF_uparrow newcommandFunF_downarrow newcommandFZliF_swarrow newcommandFZreF_nearrow newcommandFZliliF_swarrowleftarrow newcommandFZliunF_swarrowdownarrow newcommandFZrereF_nearrowrightarrow newcommandFZreobF_nearrowuparrow Es muss sowohl in horizontale als in vertikale Richtung Kräftegleichgewicht herrschen: center multicols edt Fli &mustbe Fre FZlili FZrere FZlicosalpha FZrecosbeta ed edt Fob &mustbe Fun FZreob FG + FZliun FZre sinbeta FG + FZlisinalpha ed multicols center Die untersten beiden Gleichungen bilden ein Gleichungssystem mit den Unbekannten FZli und FZre: al FZlicosalpha FZrecosbeta FZre sinbeta FG + FZlisinalpha. Wir lösen die eine Gleichung egal welche -- wir wählen die erste weil sie einfacher aussieht nach der einen Unbekannten egal welche -- wir wählen FZli auf: al FZlicosalpha FZrecosbeta uf:cosalpha FZli fracFZrecosbetacosalpha. Diesen Ausdruck setzen wir in die andere Gleichung ein und lösen nach der anderen Unbekannten FZre auf: al FZre sinbeta FG + FZlisinalpha es FZre sinbeta FG + fracFZrecosbetacosalpha sinalpha tu FZre sinbeta FG + FZrecosbeta tanalpha uf-FZrecosbetatanalpha FZresinbeta - cosbetatanalpha FG uf:sinbeta - cosbetatanalpha FZre fracFGsinbeta - cosbetatanalpha frac.eNsindegree - cosdegree tandegree .kN Wir setzen das Ergebnis in die nach der anderen Unbekannten FZli aufgelösten Gleichung ein: al FZli fracFZrecosbetacosalpha frac.eN cosdegreecosdegree .kN.
Meta Information
Exercise:
Am Tragseil eines Sessellifts hängt eine Last von .kN zwischen zwei Stützen. Der untere Teil des Seiles bildet mit der Horizontalen den Winkel ang der obere Teil den Winkel ang. Wie gross sind die Zugkräfte im oberen bzw. unteren Abschnitt des Seiles? center tikzpicturescale. filldrawfillblue!!white --. arc::.--cycle; filldrawfillblue!!white ---. arc::.--cycle; node at .. ang; node at -.-. ang; drawthick --..; drawthick ----; draw ---.--.-.--.-.---.-.; drawcolorblack!!white ..--.; drawcolorblack!!white ..--.; tikzpicture center
Solution:
newcommandFreF_rightarrow newcommandFliF_leftarrow newcommandFobF_uparrow newcommandFunF_downarrow newcommandFZliF_swarrow newcommandFZreF_nearrow newcommandFZliliF_swarrowleftarrow newcommandFZliunF_swarrowdownarrow newcommandFZrereF_nearrowrightarrow newcommandFZreobF_nearrowuparrow Es muss sowohl in horizontale als in vertikale Richtung Kräftegleichgewicht herrschen: center multicols edt Fli &mustbe Fre FZlili FZrere FZlicosalpha FZrecosbeta ed edt Fob &mustbe Fun FZreob FG + FZliun FZre sinbeta FG + FZlisinalpha ed multicols center Die untersten beiden Gleichungen bilden ein Gleichungssystem mit den Unbekannten FZli und FZre: al FZlicosalpha FZrecosbeta FZre sinbeta FG + FZlisinalpha. Wir lösen die eine Gleichung egal welche -- wir wählen die erste weil sie einfacher aussieht nach der einen Unbekannten egal welche -- wir wählen FZli auf: al FZlicosalpha FZrecosbeta uf:cosalpha FZli fracFZrecosbetacosalpha. Diesen Ausdruck setzen wir in die andere Gleichung ein und lösen nach der anderen Unbekannten FZre auf: al FZre sinbeta FG + FZlisinalpha es FZre sinbeta FG + fracFZrecosbetacosalpha sinalpha tu FZre sinbeta FG + FZrecosbeta tanalpha uf-FZrecosbetatanalpha FZresinbeta - cosbetatanalpha FG uf:sinbeta - cosbetatanalpha FZre fracFGsinbeta - cosbetatanalpha frac.eNsindegree - cosdegree tandegree .kN Wir setzen das Ergebnis in die nach der anderen Unbekannten FZli aufgelösten Gleichung ein: al FZli fracFZrecosbetacosalpha frac.eN cosdegreecosdegree .kN.
Am Tragseil eines Sessellifts hängt eine Last von .kN zwischen zwei Stützen. Der untere Teil des Seiles bildet mit der Horizontalen den Winkel ang der obere Teil den Winkel ang. Wie gross sind die Zugkräfte im oberen bzw. unteren Abschnitt des Seiles? center tikzpicturescale. filldrawfillblue!!white --. arc::.--cycle; filldrawfillblue!!white ---. arc::.--cycle; node at .. ang; node at -.-. ang; drawthick --..; drawthick ----; draw ---.--.-.--.-.---.-.; drawcolorblack!!white ..--.; drawcolorblack!!white ..--.; tikzpicture center
Solution:
newcommandFreF_rightarrow newcommandFliF_leftarrow newcommandFobF_uparrow newcommandFunF_downarrow newcommandFZliF_swarrow newcommandFZreF_nearrow newcommandFZliliF_swarrowleftarrow newcommandFZliunF_swarrowdownarrow newcommandFZrereF_nearrowrightarrow newcommandFZreobF_nearrowuparrow Es muss sowohl in horizontale als in vertikale Richtung Kräftegleichgewicht herrschen: center multicols edt Fli &mustbe Fre FZlili FZrere FZlicosalpha FZrecosbeta ed edt Fob &mustbe Fun FZreob FG + FZliun FZre sinbeta FG + FZlisinalpha ed multicols center Die untersten beiden Gleichungen bilden ein Gleichungssystem mit den Unbekannten FZli und FZre: al FZlicosalpha FZrecosbeta FZre sinbeta FG + FZlisinalpha. Wir lösen die eine Gleichung egal welche -- wir wählen die erste weil sie einfacher aussieht nach der einen Unbekannten egal welche -- wir wählen FZli auf: al FZlicosalpha FZrecosbeta uf:cosalpha FZli fracFZrecosbetacosalpha. Diesen Ausdruck setzen wir in die andere Gleichung ein und lösen nach der anderen Unbekannten FZre auf: al FZre sinbeta FG + FZlisinalpha es FZre sinbeta FG + fracFZrecosbetacosalpha sinalpha tu FZre sinbeta FG + FZrecosbeta tanalpha uf-FZrecosbetatanalpha FZresinbeta - cosbetatanalpha FG uf:sinbeta - cosbetatanalpha FZre fracFGsinbeta - cosbetatanalpha frac.eNsindegree - cosdegree tandegree .kN Wir setzen das Ergebnis in die nach der anderen Unbekannten FZli aufgelösten Gleichung ein: al FZli fracFZrecosbetacosalpha frac.eN cosdegreecosdegree .kN.
Contained in these collections:
-
Sessellift by TeXercises
-
Kraft als Vektor 2 by uz
-
Kraft als Vektor II by pw
-
Trigonometrie und Zugkraft by aej
-
Kraft als Vektor by aej

